Overview

In the previous post we looked at the process of generating a 2D bounding box around some data/cluster of points. But while working with LIDARs i.e. point cloud data respectively, we would want the bounding boxes to be in 3-dimensions just like the data.

2D Oriented bounding boxes recap

As a quick recap, the steps involved in generating 2D oriented box is as follows-

  1. Translate the data to match the means to the origin
  2. Calculate the Eigen-vectors
  3. Find the inclination/orientation angle of the principal component i.e. the Eigen-vector with highes Eigen-value
  4. Use the angle calculated in step 3 to align the data/Eigen-vectors to the cartesian basis vectors
  5. Calculate the bounding box by determining the max, min values along each dimension
  6. Undo the rotation and translation to both data and bounding box coordinates

Notes on difference in procedure to 3D oriented bounding boxes

Here we notice that Eigen-vectors, translation, and rotation tasks play the main role. Calculating Eigen-vectors and performing translation is a straight forward task in 3D also but rotation is not. As, rotation around orthogonal axis is not commutative i.e. the order in which the layers of a Rubiks cube are rotated matters. That is changing the order in which the layers are rotated will result in a completely different colour patterns on the Rubiks cube. This non-commutative nature of rotations is shown below (feel free to skip to the next section if you are already aware of this)

Handle some imports and set seed for the random generator 

%matplotlib widget
import matplotlib.pyplot as plt
import numpy as np
import numpy.linalg as LA
from mpl_toolkits.mplot3d import Axes3D

Roll, Pitch, and Yaw matrices

Here we define the yaw(rotation about z axis), pitch(rotation about y axis), and roll(rotation about x axis) matrices to see the effects of rotating a vector (2, 0, 0) and prove that rotations are not commutative in nature.

def yaw(theta):
    theta = np.deg2rad(theta)
    return np.array([[np.cos(theta), -np.sin(theta), 0],
                     [np.sin(theta),  np.cos(theta), 0],
                     [            0,              0, 1]])

def pitch(theta):
    theta = np.deg2rad(theta)
    return np.array([[np.cos(theta) , 0, np.sin(theta)],
                     [             0, 1,             0],
                     [-np.sin(theta), 0, np.cos(theta)]])

def roll(theta):
    theta = np.deg2rad(theta)
    return np.array([[1,              0,             0],
                     [0,  np.cos(theta), np.sin(theta)],
                     [0, -np.sin(theta), np.cos(theta)]])

def CreateFigure():
    """
    Helper function to create figures and label axes
    """
    fig = plt.figure()
    ax = fig.add_subplot(111, projection='3d')
    ax.set_xlabel('x')
    ax.set_ylabel('y')
    ax.set_zlabel('z')
    return ax

Yaw

Rotate vector (2, 0, 0) by 90 degrees anti-clockwise around z axis

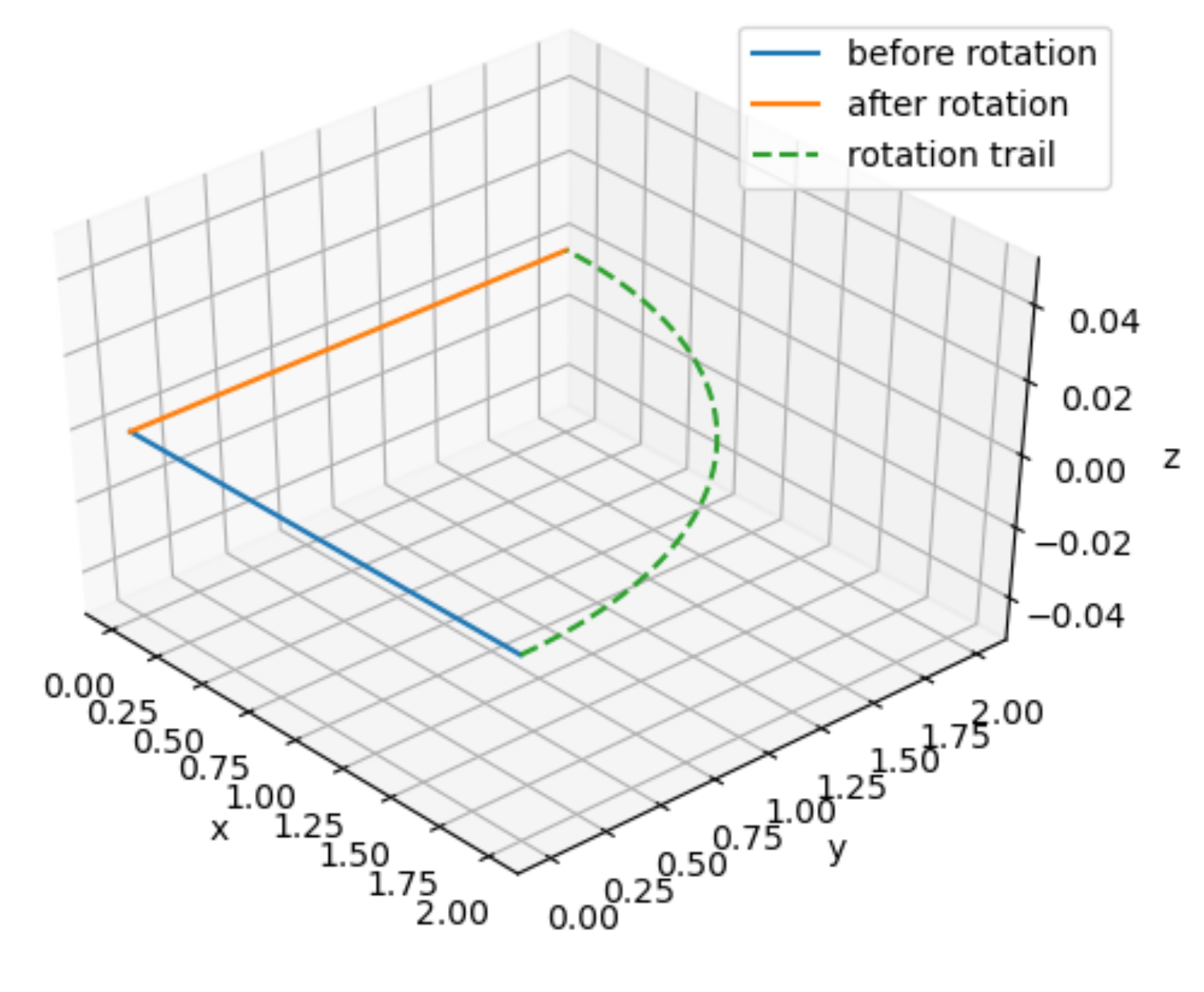
x = np.matmul(yaw(90), np.array([[2],
                                 [0],
                                 [0]]))

ax = CreateFigure()

ax.plot([0, 2], [0, 0], [0, 0], label="before rotation")
ax.plot([0, x[0,0]], [0, x[1,0]], [0, x[2,0]], label="after rotation")
ax.plot(2 * np.cos(np.linspace(0, np.pi/2, 50)), 2 * np.sin(np.linspace(0, np.pi/2, 50)), 0, linestyle="dashed", label="rotation trail")
ax.legend()

Roll

Rotate vector (2, 0, 0) by 90 degrees anti-clockwise around x axis

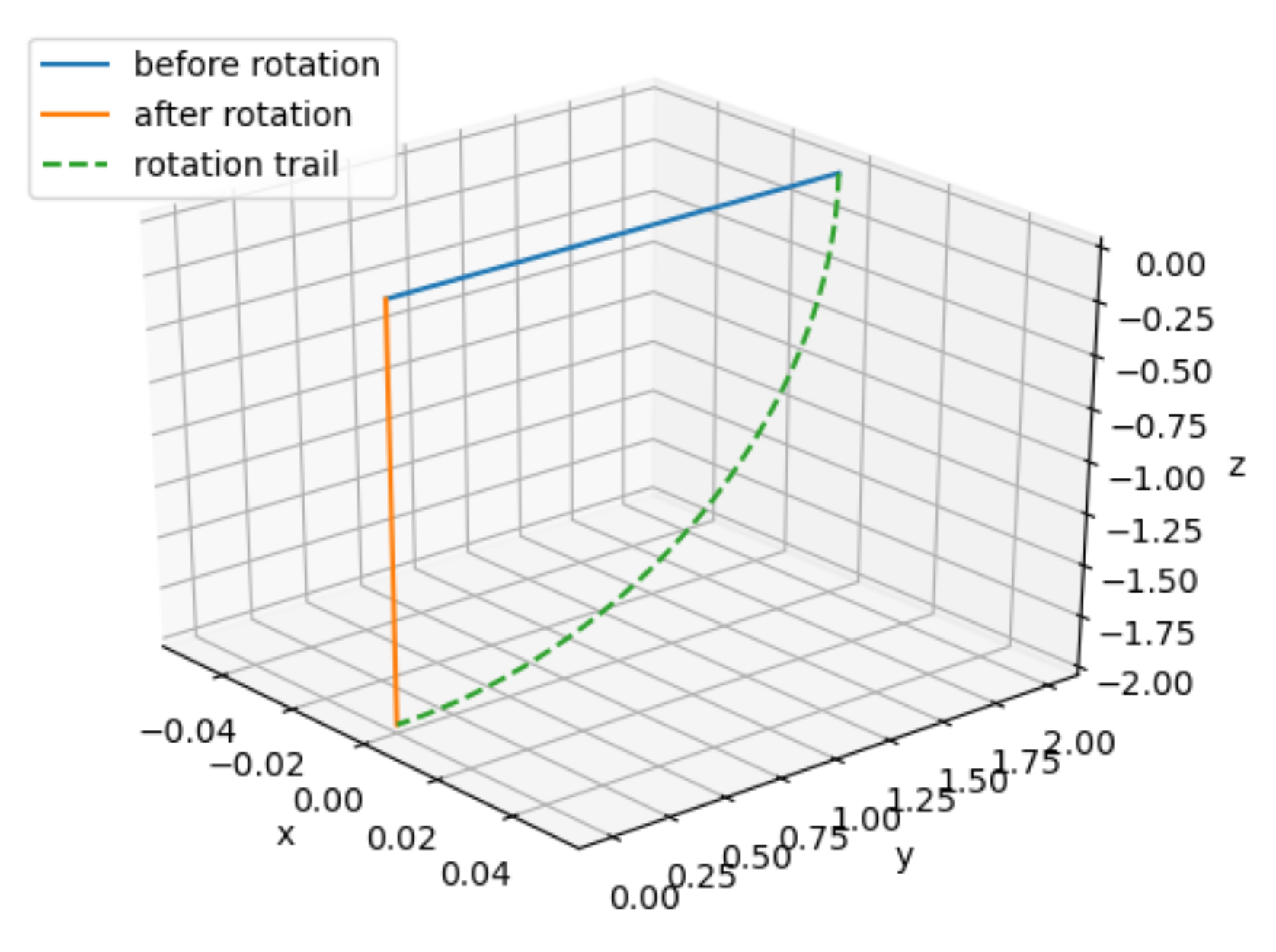
x = np.matmul(roll(90), np.array([[0],
                                  [2],
                                  [0]]))

ax = CreateFigure()

ax.plot([0, 0], [0, 2], [0, 0], label="before rotation")
ax.plot([0, x[0,0]], [0, x[1,0]], [0, x[2,0]], label="after rotation")
ax.plot(np.zeros(50), 2 * np.cos(np.linspace(0, np.pi/2, 50)), -2 * np.sin(np.linspace(0, np.pi/2, 50)), linestyle="dashed", label="rotation trail")
ax.legend()

Pitch

Rotate point (2, 0) by 90 degrees anti-clockwise around y axis

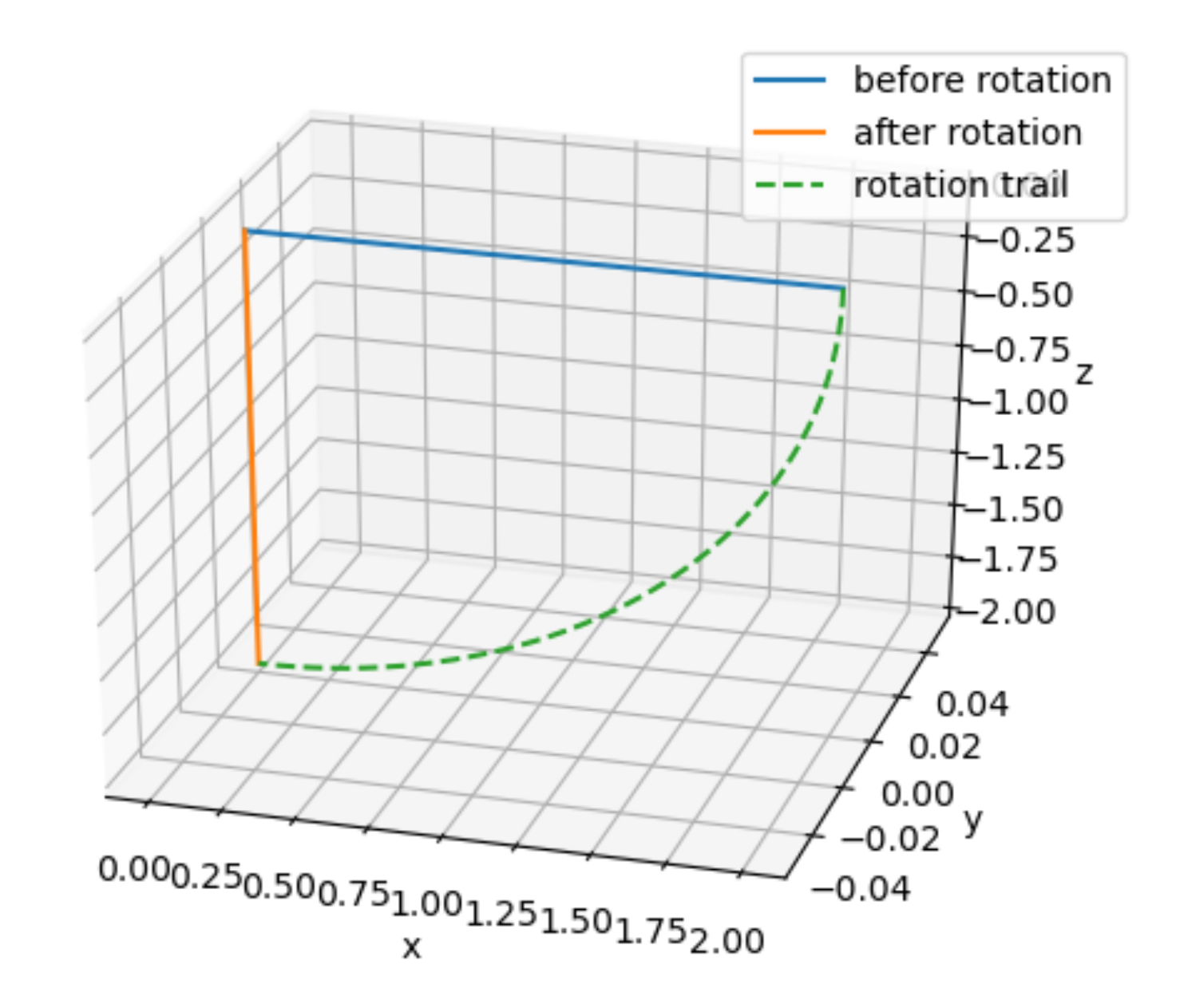
x = np.matmul(pitch(90), np.array([[2],
                                   [0],
                                   [0]]))

ax = CreateFigure()

ax.plot([0, 2], [0, 0], [0, 0], label="before rotation")
ax.plot([0, x[0,0]], [0, x[1,0]], [0, x[2,0]], label="after rotation")
ax.plot(2 * np.cos(np.linspace(0, np.pi/2, 50)), np.zeros(50), -2 * np.sin(np.linspace(0, np.pi/2, 50)), linestyle="dashed", label="rotation trail")
ax.legend()

Roll, Pitch, and Yaw together and the non-commutative nature of rotations visualised 

basis = np.array([[1,0,0],
                  [0,1,0],
                  [0,0,1]])
x1 = np.matmul(yaw(90) @ pitch(90), np.array([[2], [0], [0]]))
x2 = np.matmul(pitch(90) @ yaw(90), np.array([[2], [0], [0]]))

def SetAxisProp(ax):
    ax.set_xlabel('x')
    ax.set_ylabel('y')
    ax.set_zlabel('z')
    ax.set_xlim(-2, 2)
    ax.set_ylim(-2, 2)
    ax.set_zlim(-2, 2)
    
fig = plt.figure(figsize=(10,6))
ax1 = fig.add_subplot(121, projection='3d')
SetAxisProp(ax1)
ax2 = fig.add_subplot(122, projection='3d')
SetAxisProp(ax2)

ax1.set_title("Yaw x Pitch")
ax1.plot([0, 2], [0, 0], [0, 0], label="before rotation")
ax1.plot([0, x1[0,0]], [0, x1[1,0]], [0, x1[2,0]], label="after rotation")
ax1.legend()

ax2.set_title("Pitch x Yaw")
ax2.plot([0, 2], [0, 0], [0, 0], label="before rotation")
ax2.plot([0, x2[0,0]], [0, x2[1,0]], [0, x2[2,0]], label="after rotation")
ax2.legend()

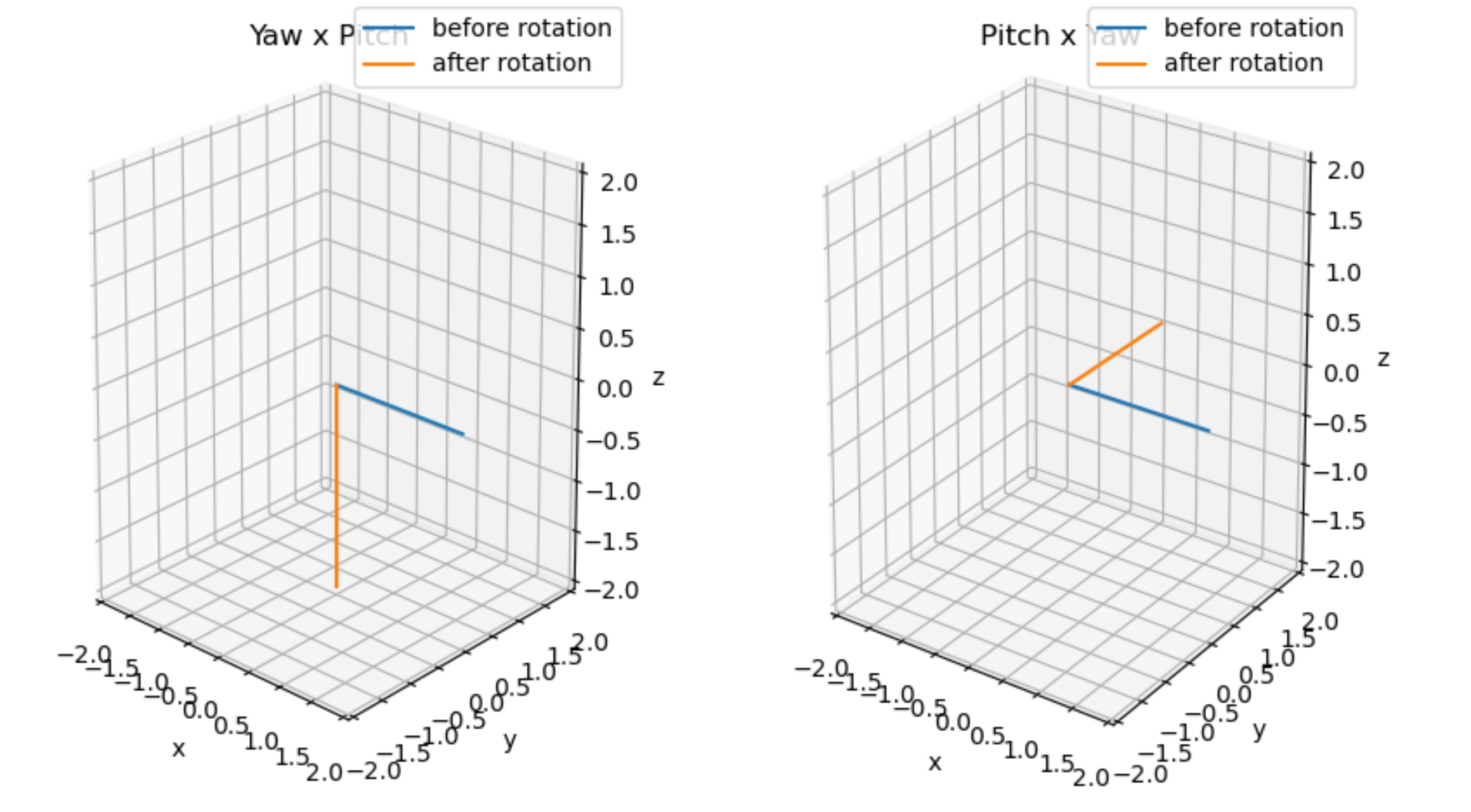
As we can see in the figure above, just changing the order in which yaw and pitch the vector, the resulting vector is completely different!

So, in this post the main difference compared to the previous post involving 2D oriented bounding boxes would be concerned with rotation and the way we align the data to the cartesian basis.

A quick overiew of what is to come

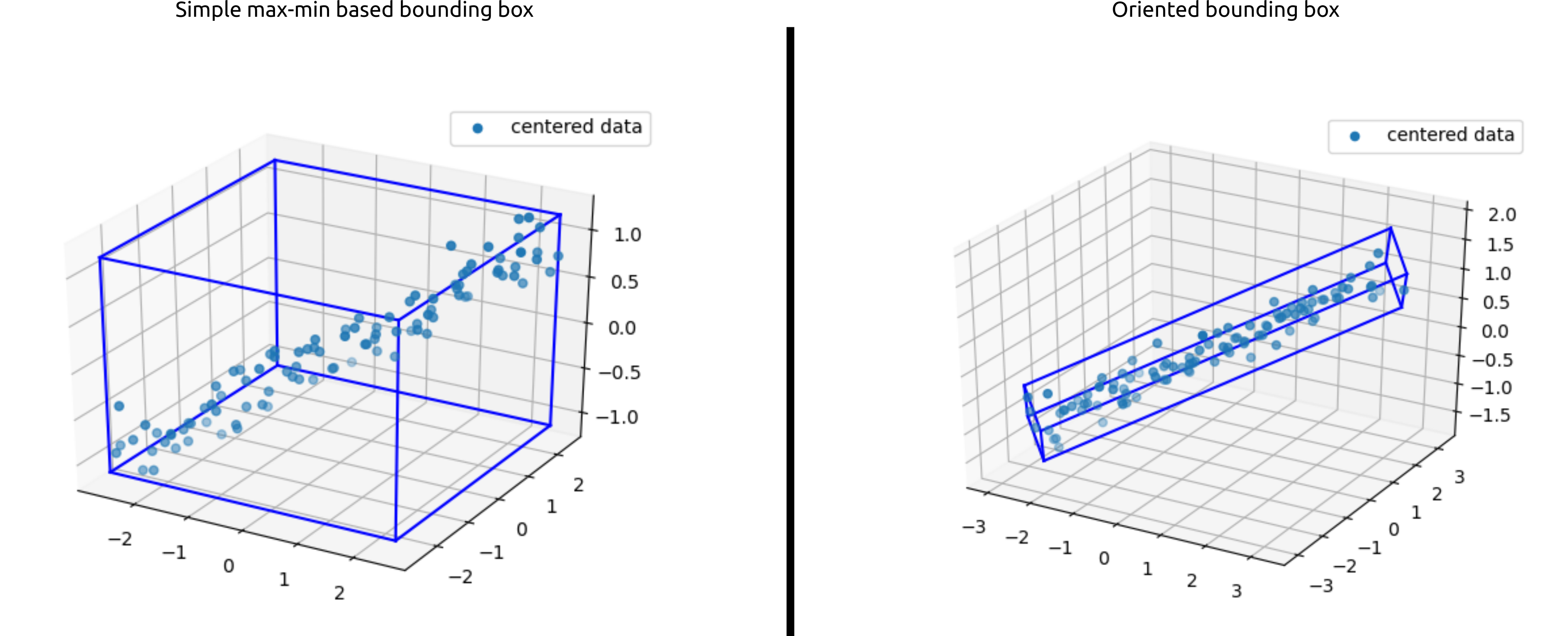
Let us get started with the code and the math to generate a bounding box

Generate 3D sample data and visualise it 

x = np.linspace(3, 8, 100) + np.random.normal(0, 0.2, 100)
y = np.linspace(3, 8, 100) + np.random.normal(0, 0.2, 100)
z = np.linspace(1, 3, 100) + np.random.normal(0, 0.2, 100)
data = np.vstack([x, y, z])

fig = plt.figure()
ax = fig.add_subplot(111, projection='3d')
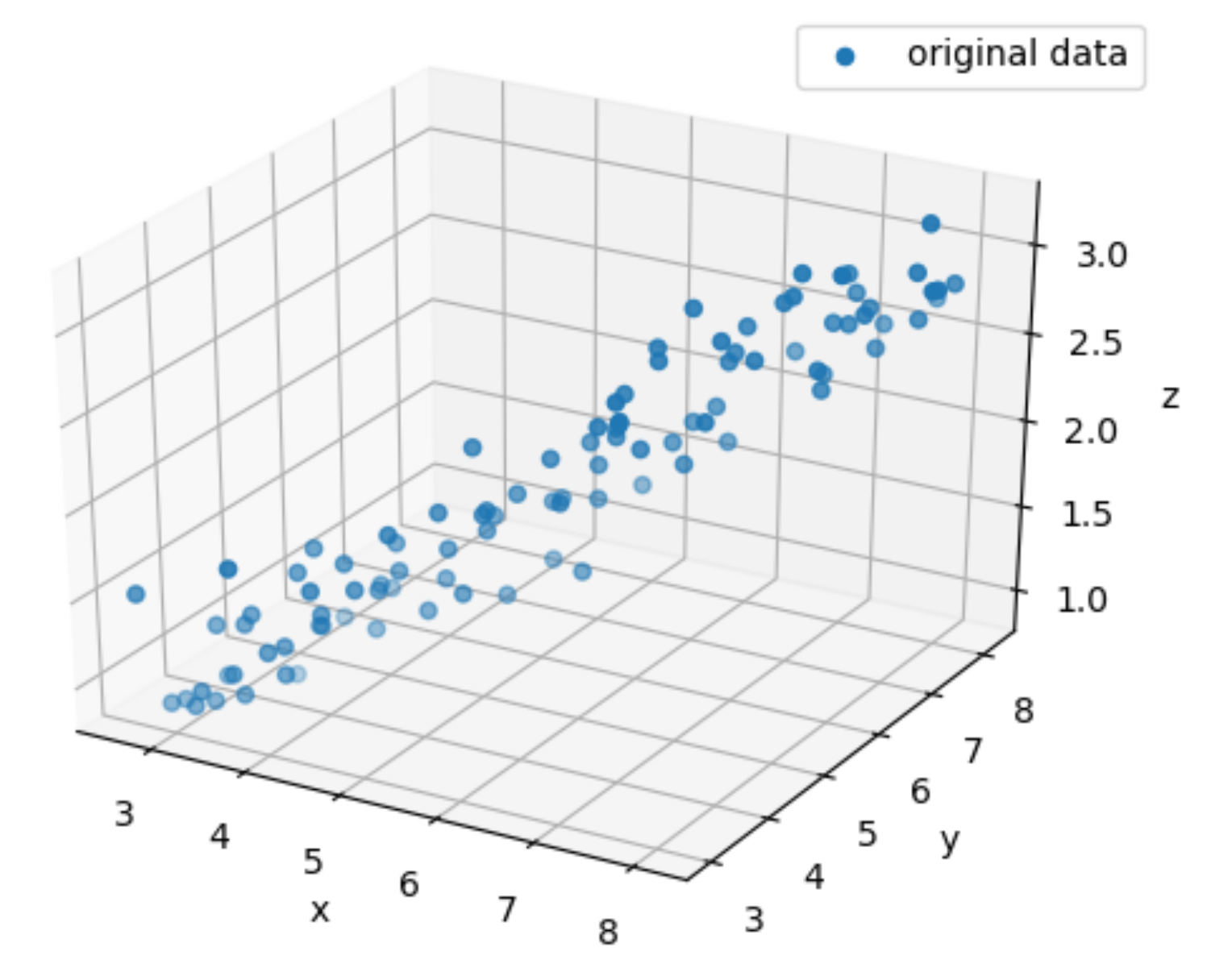
ax.scatter(data[0,:], data[1,:], data[2,:], label="original data")
ax.set_xlabel('x')
ax.set_ylabel('y')
ax.set_zlabel('z')
ax.legend()

Calculate means, covariance matrix, eigen values, and eigen vectors for the rotated data 

means = np.mean(data, axis=1)
cov = np.cov(data)
eval, evec = LA.eig(cov)
eval, evec

(array([4.74618325, 0.0445827 , 0.03395297]),
 array([[-0.68725458, -0.52695506, -0.4999995 ],
        [-0.67558502,  0.71661269,  0.1733526 ],
        [-0.26695696, -0.45692954,  0.84849831]]))

Check angle between eigen vectors

Since the Eigen-vectors returned by LA.eig are pre normalised, we can determine the angle between the eigen vectors using the dot product

np.rad2deg(np.arccos(np.dot(evec[:,0], evec[:,1])))

89.99999999999997
np.rad2deg(np.arccos(np.dot(evec[:,1], evec[:,2])))

89.99999999999976
np.rad2deg(np.arccos(np.dot(evec[:,2], evec[:,0])))

90.0

Translate the data 

centered_data = data - means[:,np.newaxis]

fig = plt.figure()
ax = fig.add_subplot(111, projection='3d')
ax.scatter(data[0,:], data[1,:], data[2,:], label="original data")
ax.scatter(centered_data[0,:], centered_data[1,:], centered_data[2,:], label="centered data")
ax.legend()
# cartesian basis
ax.plot([0, 1],  [0, 0], [0, 0], color='b', linewidth=4)
ax.plot([0, 0],  [0, 1], [0, 0], color='b', linewidth=4)
ax.plot([0, 0],  [0, 0], [0, 1], color='b', linewidth=4)
# eigen basis
ax.plot([0, evec[0, 0]],  [0, evec[1, 0]], [0, evec[2, 0]], color='r', linewidth=4)
ax.plot([0, evec[0, 1]],  [0, evec[1, 1]], [0, evec[2, 1]], color='g', linewidth=4)
ax.plot([0, evec[0, 2]],  [0, evec[1, 2]], [0, evec[2, 2]], color='k', linewidth=4)

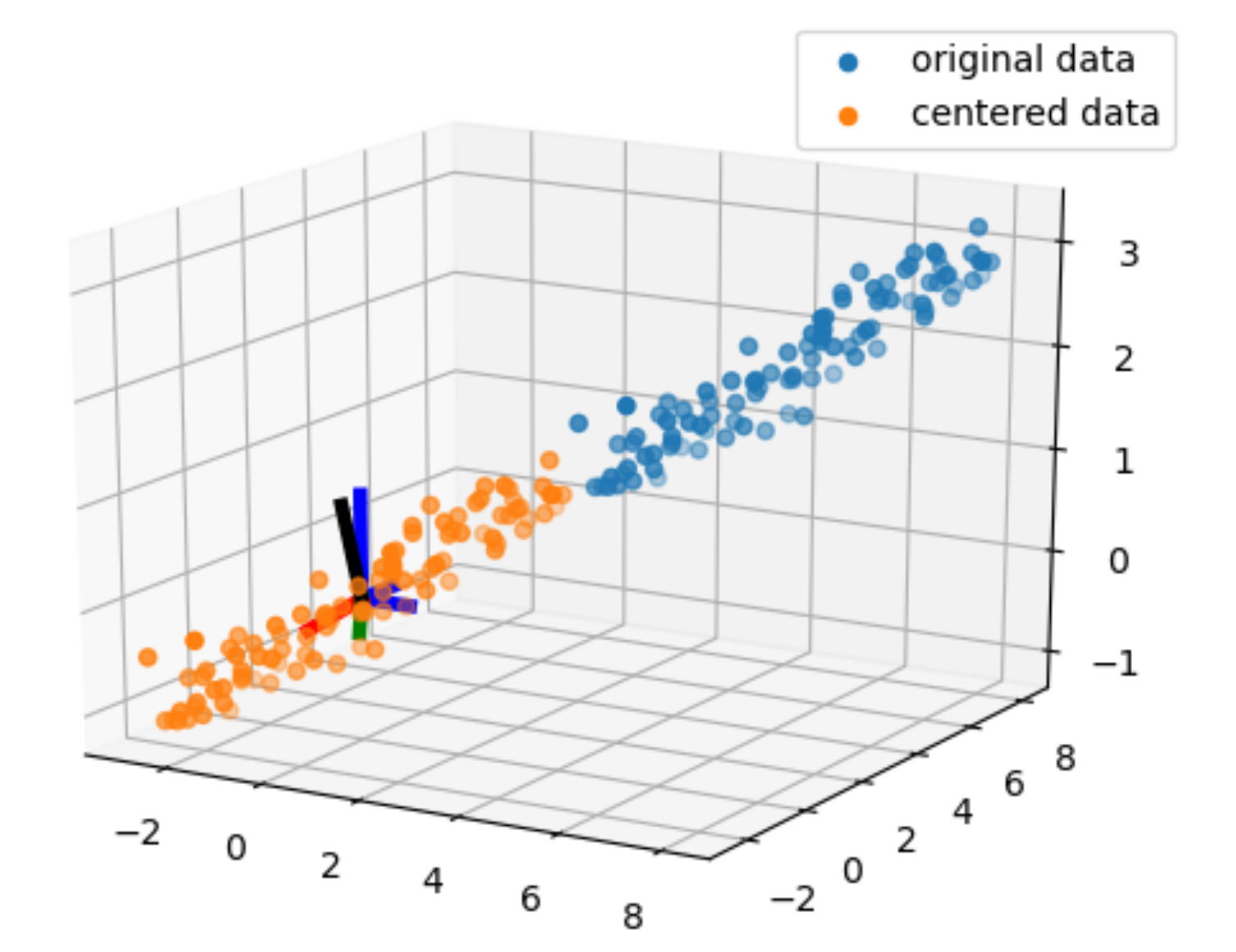
The axis orthogonal axes in blue are the cartesian basis and the ones in red, green, and black are the orthogonal eigen vector

Simple max and min based bounding box 

def draw3DRectangle(ax, x1, y1, z1, x2, y2, z2):
    # the Translate the datatwo sets of coordinates form the apposite diagonal points of a cuboid
    ax.plot([x1, x2], [y1, y1], [z1, z1], color='b') # | (up)
    ax.plot([x2, x2], [y1, y2], [z1, z1], color='b') # -->
    ax.plot([x2, x1], [y2, y2], [z1, z1], color='b') # | (down)
    ax.plot([x1, x1], [y2, y1], [z1, z1], color='b') # <--

    ax.plot([x1, x2], [y1, y1], [z2, z2], color='b') # | (up)
    ax.plot([x2, x2], [y1, y2], [z2, z2], color='b') # -->
    ax.plot([x2, x1], [y2, y2], [z2, z2], color='b') # | (down)
    ax.plot([x1, x1], [y2, y1], [z2, z2], color='b') # <--
    
    ax.plot([x1, x1], [y1, y1], [z1, z2], color='b') # | (up)
    ax.plot([x2, x2], [y2, y2], [z1, z2], color='b') # -->
    ax.plot([x1, x1], [y2, y2], [z1, z2], color='b') # | (down)
    ax.plot([x2, x2], [y1, y1], [z1, z2], color='b') # <--

Compute the minimums and maximums of each dimension and draw the rectangle 

xmin, xmax, ymin, ymax, zmin, zmax = np.min(centered_data[0, :]), np.max(centered_data[0, :]), np.min(centered_data[1, :]), np.max(centered_data[1, :]), np.min(centered_data[2, :]), np.max(centered_data[2, :])
# Code repeat start
fig = plt.figure()
ax = fig.add_subplot(111, projection='3d')
ax.scatter(data[0,:], data[1,:], data[2,:], label="original data")
ax.scatter(centered_data[0,:], centered_data[1,:], centered_data[2,:], label="centered data")
ax.legend()
# cartesian basis
ax.plot([0, 1],  [0, 0], [0, 0], color='b', linewidth=4)
ax.plot([0, 0],  [0, 1], [0, 0], color='b', linewidth=4)
ax.plot([0, 0],  [0, 0], [0, 1], color='b', linewidth=4)
# eigen basis
ax.plot([0, evec[0, 0]],  [0, evec[1, 0]], [0, evec[2, 0]], color='r', linewidth=4)
ax.plot([0, evec[0, 1]],  [0, evec[1, 1]], [0, evec[2, 1]], color='g', linewidth=4)
ax.plot([0, evec[0, 2]],  [0, evec[1, 2]], [0, evec[2, 2]], color='k', linewidth=4)
# Code repeat end
draw3DRectangle(ax, xmin, ymin, zmin, xmax, ymax, zmax)

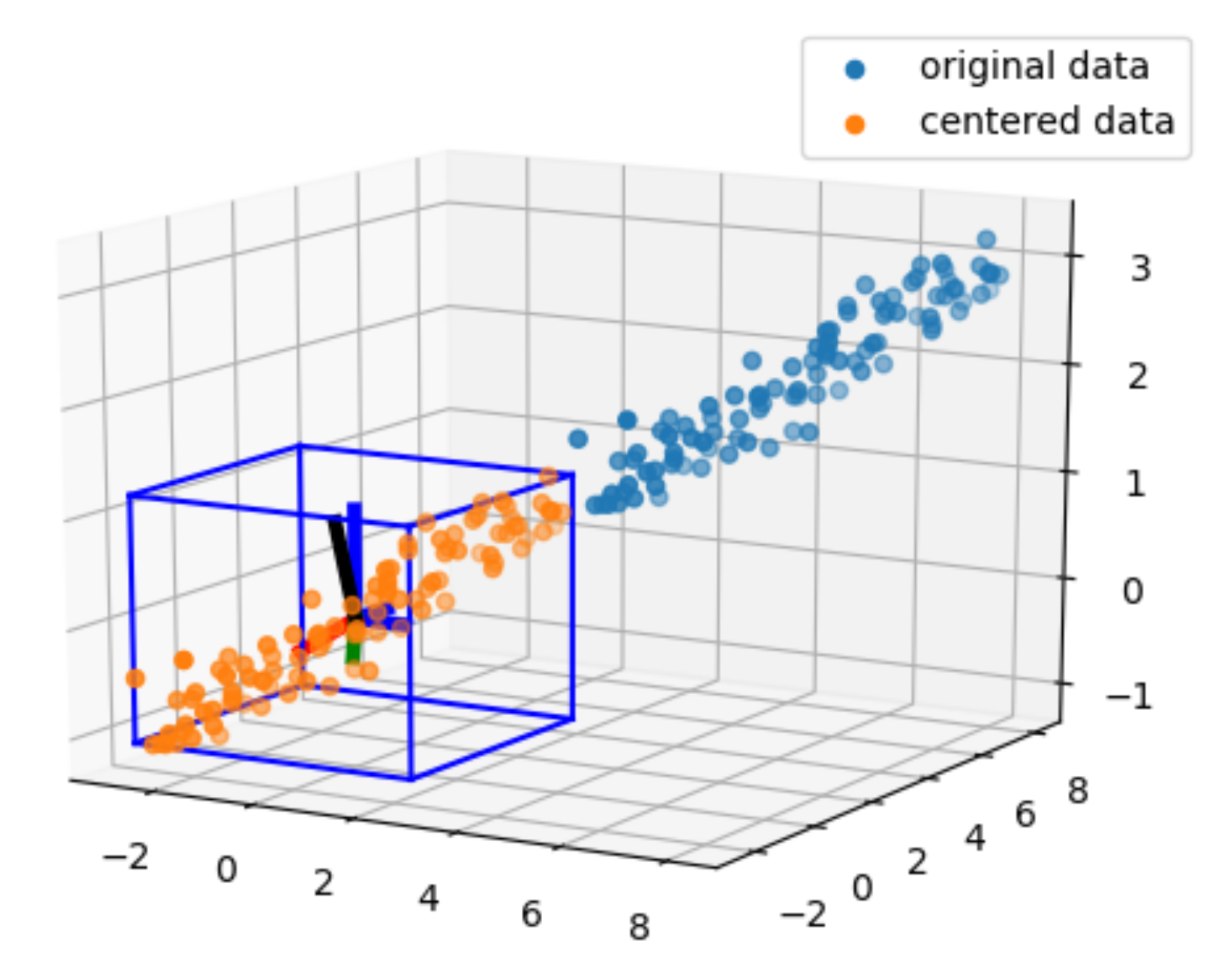
Rotation! the crux of the process in generating the oriented bounding box

As previously mentioned that the Eigen-vectors are pre normalised and that they are orthogonal to each other when we checked the angles between them, in effect we have in our hands a new set of basis vectors. We can use this basis vector to transform coordinates to and fro defined using any other basis vectors.

That is, in our case the Eigen-vectors matrix evec can be used to transform coordinates defined in the basis vectors (1,0,0), (0,1,0), (0,0,1). Let us denote the coordinates in the cartesian basis vectors as C and the coordinates with Eigen-vectors as basis as E.

  • We can transform coordinated from C to E by multiplying with the evec basis vector matrix
  • We can transform coordinated from E to C by multiplying with the inverse(evec) basis vector matrix

Since the Eigen-vectors are normalised, the inverse(evec) == transpose(evec) (the code below proves this)

np.allclose(LA.inv(evec), evec.T)

True

Rotate the data i.e. align the eigen vector to the cartesian basis 

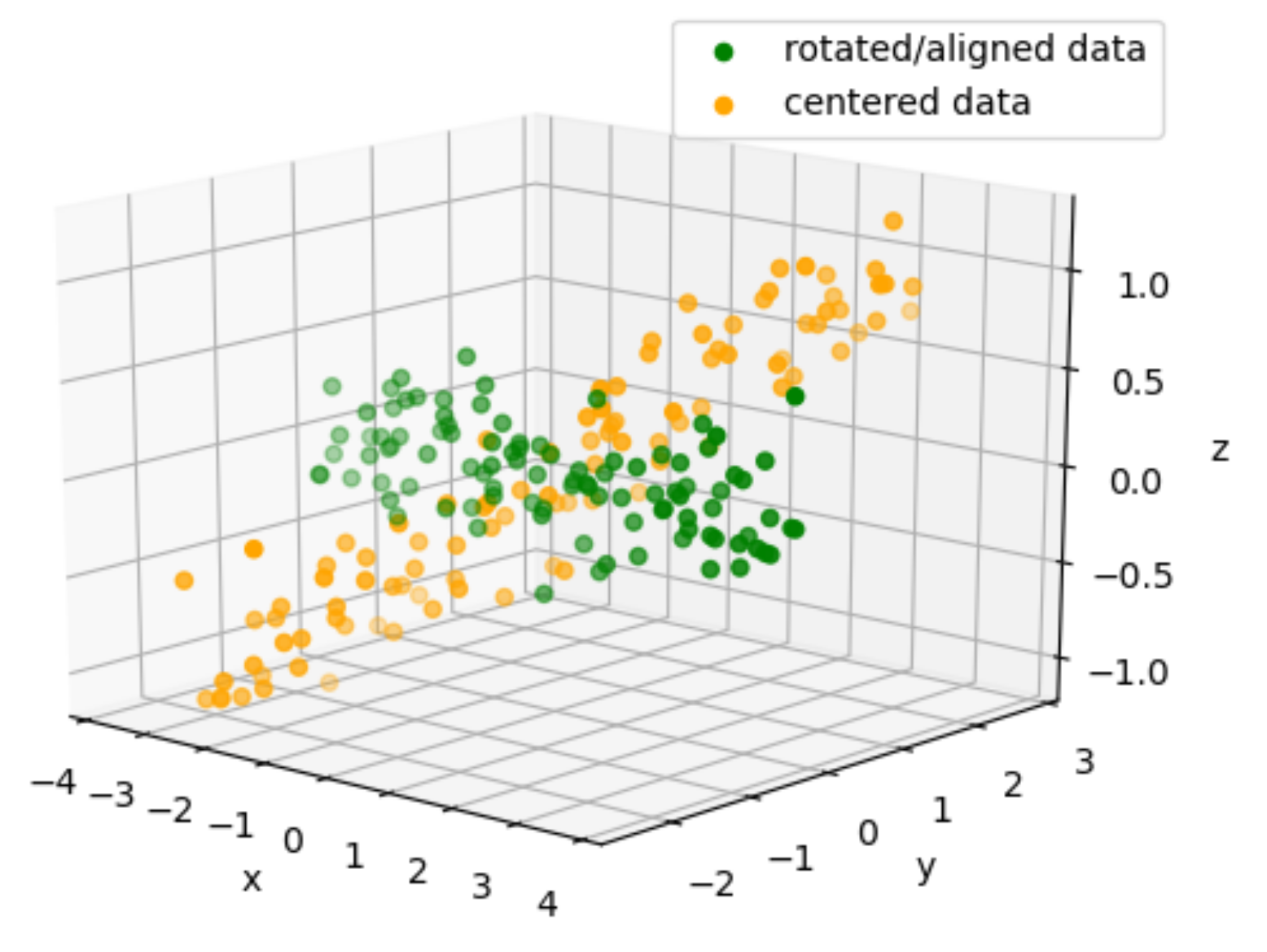
aligned_coords = np.matmul(evec.T, centered_data)

fig = plt.figure()
ax = fig.add_subplot(111, projection='3d')
ax.scatter(aligned_coords[0,:], aligned_coords[1,:], aligned_coords[2,:], color='g', label="rotated/aligned data")
ax.scatter(centered_data[0,:], centered_data[1,:], centered_data[2,:], color='orange', label="centered data")
ax.legend()
ax.set_xlabel('x')
ax.set_ylabel('y')
ax.set_zlabel('z')

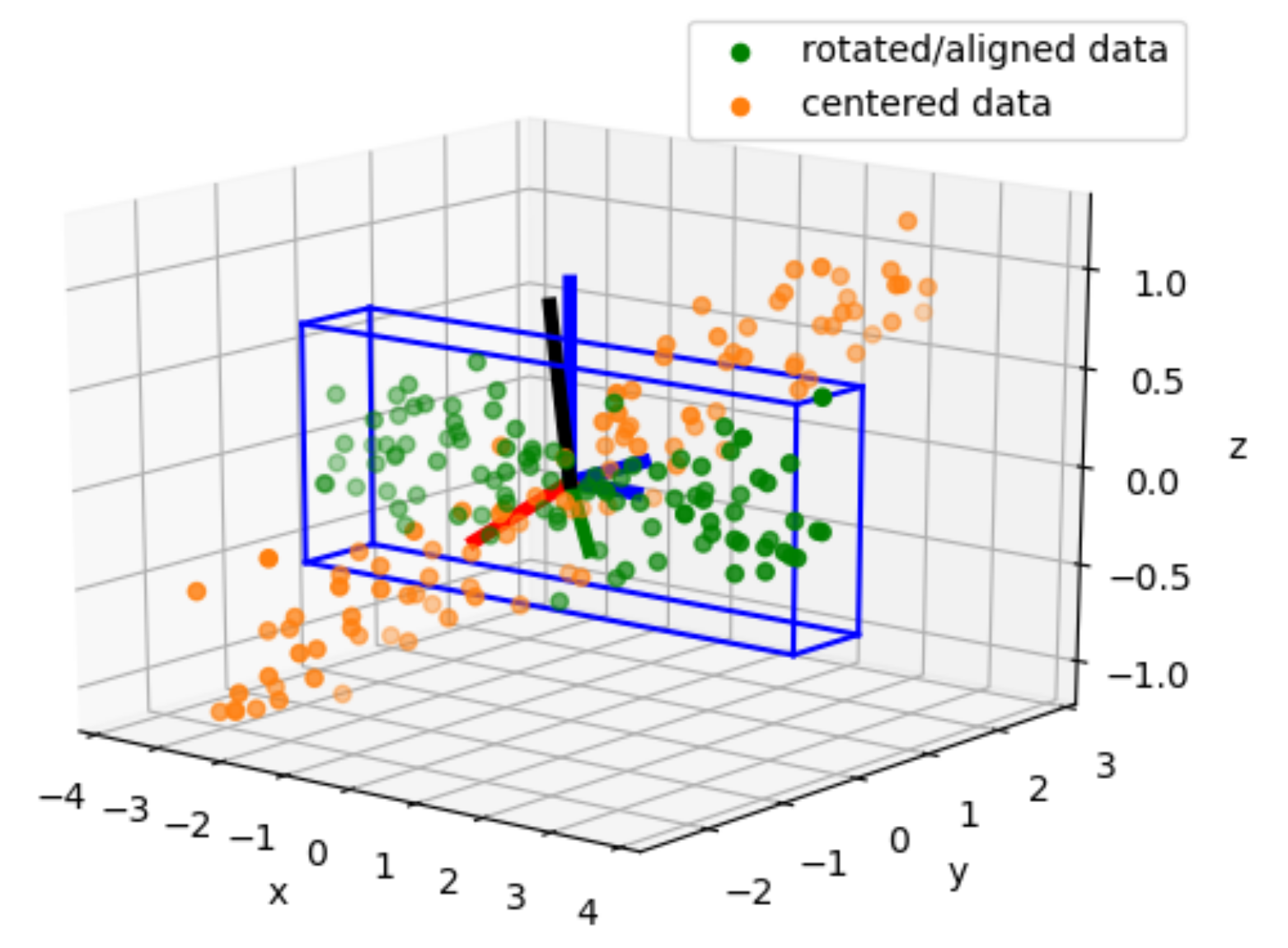
Compute the minimums and maximums of each dimension and draw the rectangle 

xmin, xmax, ymin, ymax, zmin, zmax = np.min(aligned_coords[0, :]), np.max(aligned_coords[0, :]), np.min(aligned_coords[1, :]), np.max(aligned_coords[1, :]), np.min(aligned_coords[2, :]), np.max(aligned_coords[2, :])

fig = plt.figure()
ax = fig.add_subplot(111, projection='3d')
ax.scatter(aligned_coords[0,:], aligned_coords[1,:], aligned_coords[2,:], color='g', label="rotated/aligned data")
ax.scatter(centered_data[0,:], centered_data[1,:], centered_data[2,:], color='tab:orange', label="centered data")
ax.legend()
ax.set_xlabel('x')
ax.set_ylabel('y')
ax.set_zlabel('z')
# cartesian basis
ax.plot([0, 1],  [0, 0], [0, 0], color='b', linewidth=4)
ax.plot([0, 0],  [0, 1], [0, 0], color='b', linewidth=4)
ax.plot([0, 0],  [0, 0], [0, 1], color='b', linewidth=4)
# eigen basis
ax.plot([0, evec[0, 0]],  [0, evec[1, 0]], [0, evec[2, 0]], color='r', linewidth=4)
ax.plot([0, evec[0, 1]],  [0, evec[1, 1]], [0, evec[2, 1]], color='g', linewidth=4)
ax.plot([0, evec[0, 2]],  [0, evec[1, 2]], [0, evec[2, 2]], color='k', linewidth=4)

draw3DRectangle(ax, xmin, ymin, zmin, xmax, ymax, zmax)

Undo rotation and translatation to the data and bounding box coordinates 

rectCoords = lambda x1, y1, z1, x2, y2, z2: np.array([[x1, x1, x2, x2, x1, x1, x2, x2],
                                                      [y1, y2, y2, y1, y1, y2, y2, y1],
                                                      [z1, z1, z1, z1, z2, z2, z2, z2]])

realigned_coords = np.matmul(evec, aligned_coords)
realigned_coords += means[:, np.newaxis]

rrc = np.matmul(evec, rectCoords(xmin, ymin, zmin, xmax, ymax, zmax))
# rrc = rotated rectangle coordinates

Translate the coordinates of the bounding box 

rrc += means[:, np.newaxis]

Plot the data and the bounding box 

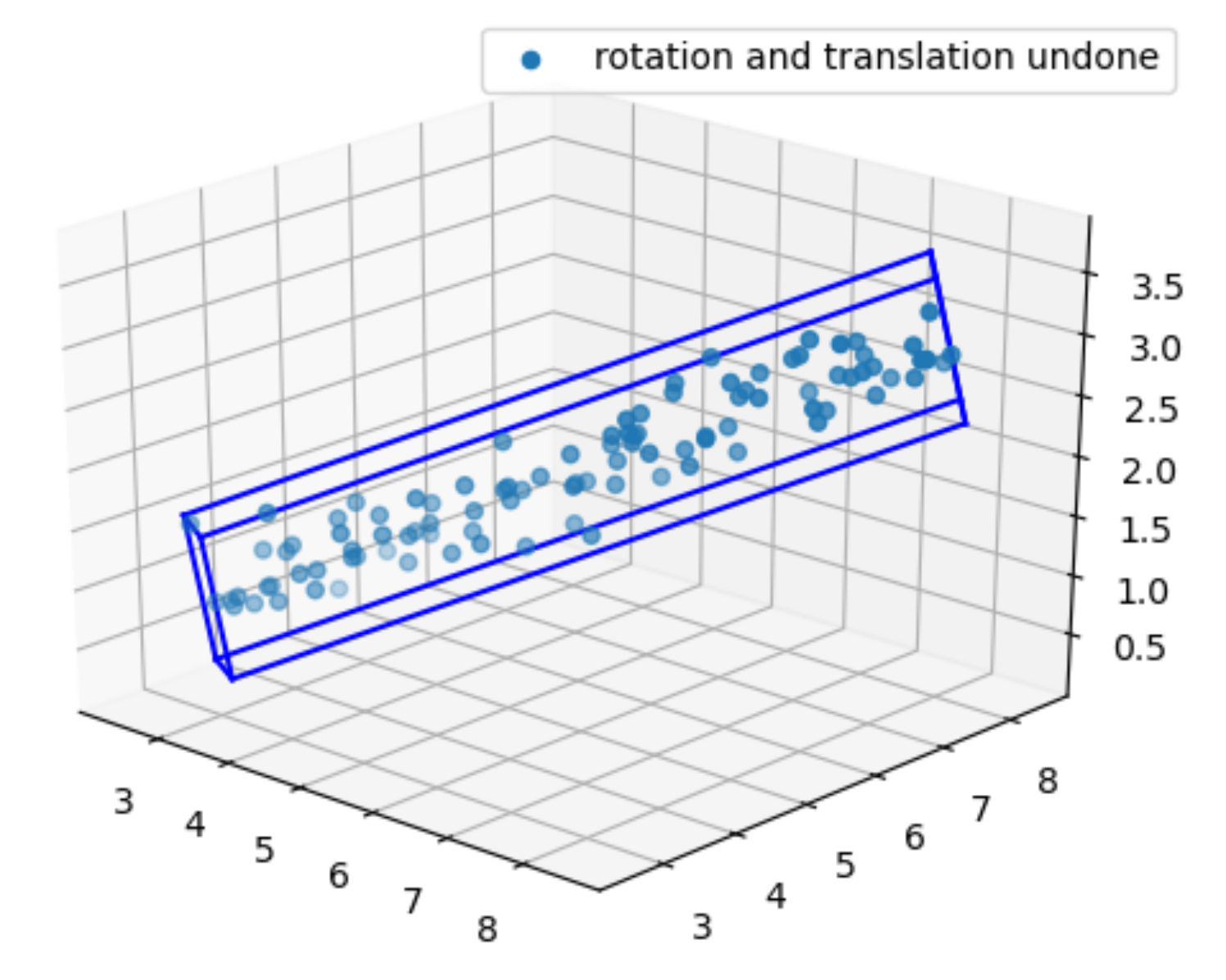
fig = plt.figure()
ax = fig.add_subplot(111, projection='3d')
ax.scatter(realigned_coords[0,:], realigned_coords[1,:], realigned_coords[2,:], label="rotation and translation undone")
ax.legend()

# z1 plane boundary
ax.plot(rrc[0, 0:2], rrc[1, 0:2], rrc[2, 0:2], color='b')
ax.plot(rrc[0, 1:3], rrc[1, 1:3], rrc[2, 1:3], color='b')
ax.plot(rrc[0, 2:4], rrc[1, 2:4], rrc[2, 2:4], color='b')
ax.plot(rrc[0, [3,0]], rrc[1, [3,0]], rrc[2, [3,0]], color='b')

# z2 plane boundary
ax.plot(rrc[0, 4:6], rrc[1, 4:6], rrc[2, 4:6], color='b')
ax.plot(rrc[0, 5:7], rrc[1, 5:7], rrc[2, 5:7], color='b')
ax.plot(rrc[0, 6:], rrc[1, 6:], rrc[2, 6:], color='b')
ax.plot(rrc[0, [7, 4]], rrc[1, [7, 4]], rrc[2, [7, 4]], color='b')

# z1 and z2 connecting boundaries
ax.plot(rrc[0, [0, 4]], rrc[1, [0, 4]], rrc[2, [0, 4]], color='b')
ax.plot(rrc[0, [1, 5]], rrc[1, [1, 5]], rrc[2, [1, 5]], color='b')
ax.plot(rrc[0, [2, 6]], rrc[1, [2, 6]], rrc[2, [2, 6]], color='b')
ax.plot(rrc[0, [3, 7]], rrc[1, [3, 7]], rrc[2, [3, 7]], color='b')

Conclusion

Using the Eigen-vectors we were able to generate a bounding box for the data we have at hand while carrying out translation, rotatation, and the conjugate operations.