Importance of reusing the results (Dynamic programming)

Problem statement: Summary

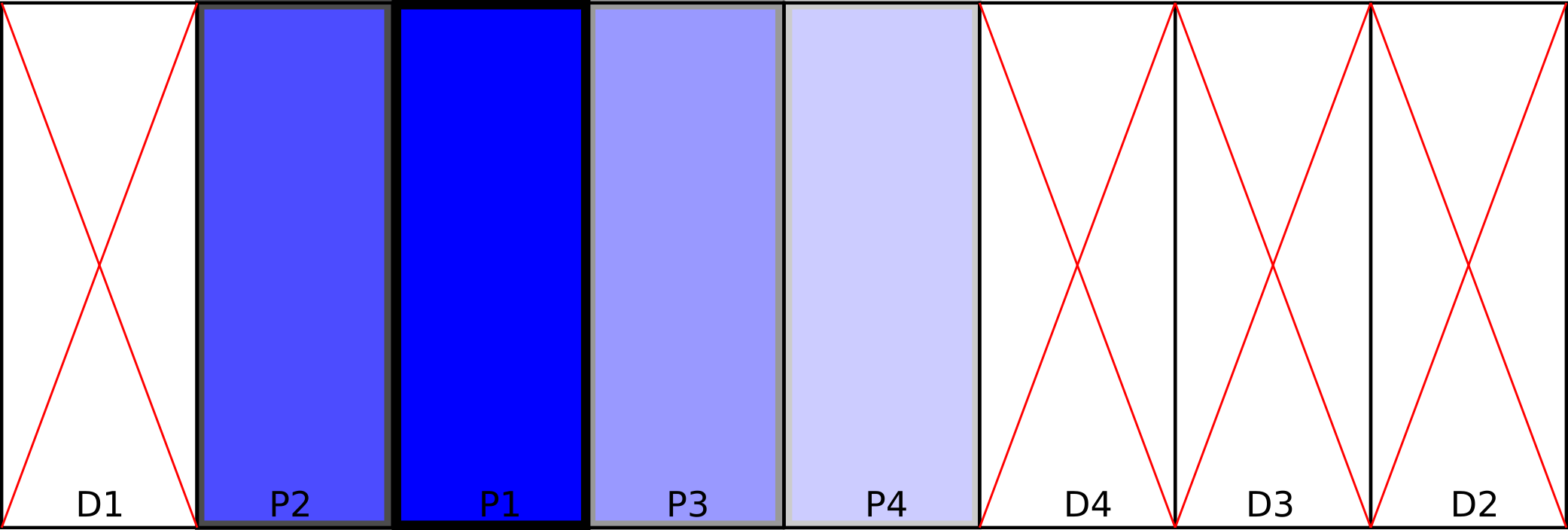Problem_explanation There are N sections on a wall and you can paint only one of the sections in a day, the next day you are allowed to paint the section which is adjacent to a painted one only. Also, everyday one section gets destroyed and the section which gets destroyed are always at the ends (adjacent to unpainted ones)

In the above figure you will see one of the many possibilities.

  • P# -> Painted section on day #
  • D# -> Destroyed section on day #

Problem description

Thanh wants to paint a wonderful mural on a wall that is N sections long. Each section of the wall has a beauty score, which indicates how beautiful it will look if it is painted. Unfortunately, the wall is starting to crumble due to a recent flood, so he will need to work fast! At the beginning of each day, Thanh will paint one of the sections of the wall. On the first day, he is free to paint any section he likes. On each subsequent day, he must paint a new section that is next to a section he has already painted, since he does not want to split up the mural. At the end of each day, one section of the wall will be destroyed. It is always a section of wall that is adjacent to only one other section and is unpainted (Thanh is using a waterproof paint, so painted sections can’t be destroyed). The total beauty of Thanh’s mural will be equal to the sum of the beauty scores of the sections he has painted. Thanh would like to guarantee that, no matter how the wall is destroyed, he can still achieve a total beauty of at least B. What’s the maximum value of B for which he can make this guarantee?

Input

The first line of the input gives the number of test cases, T. T test cases follow. Each test case starts with a line containing an integer N. Then, another line follows containing a string of N digits from 0 to 9. The i-th digit represents the beauty score of the i-th section of the wall.

Output

For each test case, output one line containing Case #x: y, where x is the test case number (starting from 1) and y is the maximum beauty score that Thanh can guarantee that he can achieve, as described above.

Limits

1 ≤ T ≤ 100. Time limit: 20 seconds per test set. Memory limit: 1 GB.

Small dataset (Test set 1 - Visible)

2 ≤ N ≤ 100.

Large dataset (Test set 2 - Hidden)

For exactly 1 case, N = 5 × 106; for the other T - 1 cases, 2 ≤ N ≤ 100. Sample

Meaning Input Output
Cases 4 Case #1: 6
#Sections 4 Case #2: 14
Beauty scores 1332 Case #3: 7
#Sections 4 Case #4: 31
Beauty scores 9583  
#Sections 3  
Beauty scores 616  
#Sections 10  
Beauty scores 1029384756  

  • In the first sample case, Thanh can get a total beauty of 6, no matter how the wall is destroyed. On the first day, he can paint either section of wall with beauty score 3. At the end of the day, either the 1st section or the 4th section will be destroyed, but it does not matter which one. On the second day, he can paint the other section with beauty score 3.

  • In the second sample case, Thanh can get a total beauty of 14, by painting the leftmost section of wall (with beauty score 9). The only section of wall that can be destroyed is the rightmost one, since the leftmost one is painted. On the second day, he can paint the second leftmost section with beauty score 5. Then the last unpainted section of wall on the right is destroyed. Note that on the second day, Thanh cannot choose to paint the third section of wall (with beauty score 8), since it is not adjacent to any other painted sections.

  • In the third sample case, Thanh can get a total beauty of 7. He begins by painting the section in the middle (with beauty score 1). Whichever section is destroyed at the end of the day, he can paint the remaining wall at the start of the second day.

Solution

Looking at the problem and the sample solutions, it is clear that the painted sections are always contiguous(next to each other as chain link) and the length of the painted sections is ceil(N/2).

The solution to the problem is quite simple in it’s own worth but the challenge is to come up with a efficient solution to solve for large number of sections!! The solution to the problem is max of the rolling sum of roll length ceil(N/2)

If you are familiar with pandas library, the solution is a one line of code if we have all the beauty scores of the wall sections in a pandas Series-

import pandas as pd
beauty_scores = pd.read_csv('input/path/to/file', delimiter=' ')
result  = pd.beauty_scores.rolling(math.ceil(N/2)).sum().max()

Read the data

wall_sections = []
beauty_scores = []

with open('../inputs/mural_2018_H.txt') as file:
    cases = int(file.readline().rstrip())
    for case in range(cases):
        wall_sections.append(int(file.readline().rstrip()))
        beauty_scores.append(list(map(int, list(file.readline().rstrip()))))

Solve the test case one by one

We first calculate the roll length and then calculate the roll sums of the beauty scores

def solve_a(sections, bs):
    if sections % 2 == 0:
        roll = sections // 2
        roll_sums = [sum(bs[i:i+roll]) for i in range(sections - roll + 1)]
    else:
        roll = sections // 2 + 1
        roll_sums = [sum(bs[i:i+roll+1]) for i in range(sections - roll)]
    return max(roll_sums)

for case in range(cases):
    result = solve(wall_sections[case], beauty_scores[case])
    print("Case #{}: {}".format(case + 1, result))

Let us have a look at the number of operations involved-

  • roll_windows = N - roll_length
  • summations = (roll_windows) * roll_length
  • comparisons = roll_windows

i.e., O(roll_windows + summations + comparisons) operations_vs_sections Note: The scales are in log

Improved solution, making use of previous results

Based on the operations breakdown we have seen just now, I see that a substantial number of summations can be avoided by utilizing the concept that every successive roll window overlaps the previous roll window except one element/beauty score 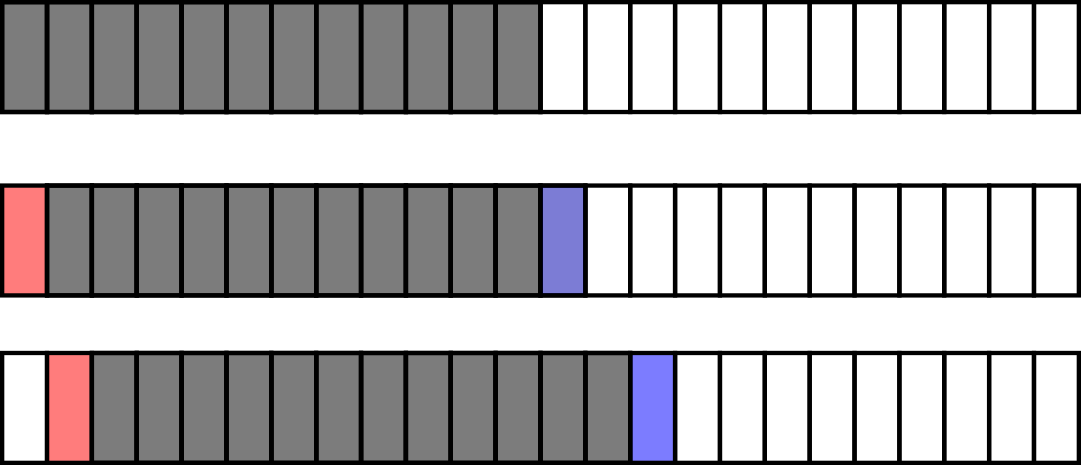roll_window To save on computations, we just have to add the beauty score of the new section and subtract which we do not want anymore.

Let us have a look at the number of operations involved-

  • roll_windows = N - roll_length
  • summations = (roll_windows) * 2
  • comparisons = roll_windows

i.e., O(roll_windows + summations + comparisons) operations_vs_sections

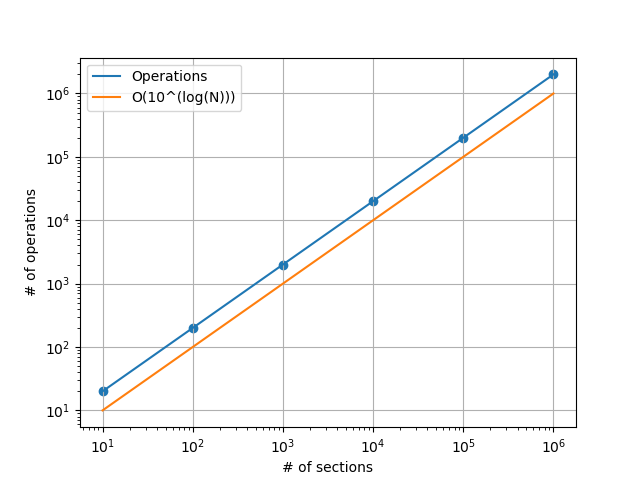
Based on the graphs it is clear that we see an improvement from O(10^(2log(N))) to O(10^log(N))

def solve_b(sections, bs):
    if sections % 2 == 0:
        roll = sections // 2
        tmp = sum(bs[:roll])
        max_value = tmp
        for i in range(1, sections - roll + 1):
            tmp = tmp + bs[i+roll-1] - bs[i-1]
            if max_value < tmp:
                max_value = tmp
        return max_value
    else:
        roll = sections // 2 + 1
        tmp = sum(bs[:roll])
        max_value = tmp
        for i in range(1, sections - roll + 1):
            tmp = tmp + bs[i + roll - 1] - bs[i - 1]
            if max_value < tmp:
                max_value = tmp
        return max_value

Time comparisons

time comparisons

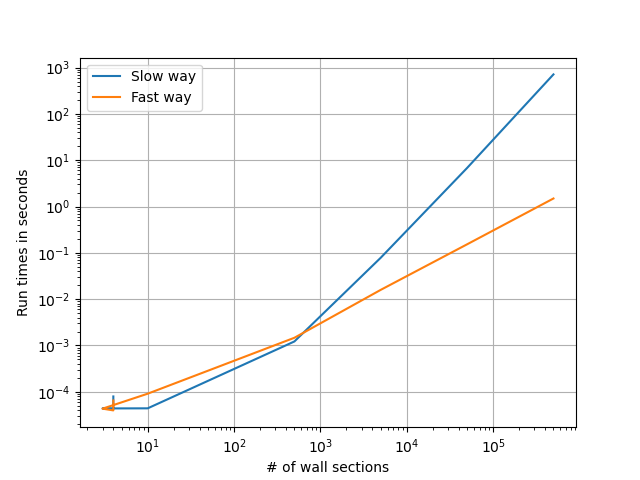
Slow(time in seconds) Fast(time in seconds) Improvement factor (times x) Wall sections
7.91e-05 6.48e-05 1.22x 4
4.24e-05 3.95e-05 1.07x 4
4.36e-05 4.31e-05 1.01x 3
4.38e-05 9.08e-05 0.48x 10
0.00121 0.00146 0.83x 500
0.0784 0.0158 4.94x 5000
6.80 0.15 44.55x 50000
712.75 1.49 478.12x 500000

Try it out

If you feel like working out or if you have a much simpler and faster approach to solving this problem, I would like to see and learn!!

Here is the link to Test input and the test results if you want to cross check

Case #1: 6
Case #2: 14
Case #3: 7
Case #4: 31
Case #5: 1012
Case #6: 10129
Case #7: 100501
Case #8: 1001276