Please use the scrollbar to the right to scroll the page down if the mouse scroll gesture doesn't work (scroll gesture also acts as a zoom-in and zoom-out in this blog post).

(Click the drag the nodes to interact with the graph) The animation shows the way the Dijikstra's algorithm progresses and searches for the destination planet/target. A collection of possible routes from one node are coloured with the same color and finally when the shortest route to the destination planet is found, the found route i.e. the solution is highlighted with RED coloured thick lines.

Betrandt AG's coding challenge

I didn't actually happen to randomly start working on this blog post. This blog post is inspired by my participation in the coding challenge organised by Betrandt AG. The entire details of the coding challenge are available here https://www.get-in-it.de/magazin/events/challenges/review-coding-in-the-galaxy

Dijikstra’s algorithm

Dijkstra’s algorithm (or Dijkstra’s Shortest Path First algorithm, SPF algorithm) is an algorithm for finding the shortest paths between nodes in a graph, which may represent, for example, road networks. It was conceived by computer scientist Edsger W. Dijkstra in 1956 and published three years later.

This particular coding challenge deals with a single source and single destination. The algorithm states to visit the child planets in the order of least cost and keep updating the path when a route with lower cost is found.

Example:

Dijkstra example

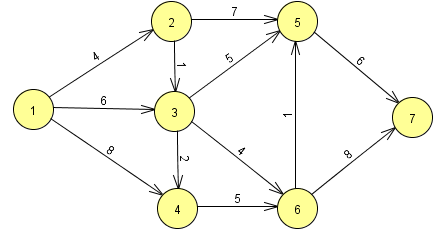
Start: at node 1

Iter: 1

To vist: [2, 3, 4] in order (children of node 1)
Parent -> [childs]
2 -> [3, 5]
3 -> [4, 5, 6]
4 -> [6]

iter: 2

To vist: [[3, 5], [4, 6, 5], [6]] in order (children of unvisited nodes only to avoid repetition)
Cost of reaching 3 via 2 is 4+1 which is less than 1 -> 3, so update the cost and path to reach 3
Cost of reaching 5 via 2 is 4+7 and this is first time we are visiting the node, so store the cost and path to reach 5
Cost of reaching 4 via 3 is 4+1+2 and this is less than 1 -> 4, so update the path and cost to reach 4
Cost of reaching 6 via 3 is 4+1+4 and this is first time we are visiting the node, so store the cost and path to reach 6
Cost of reaching 5 via 3 is now 4+1+5 which is less than 1 -> 3 -> 5 because we have updated the path to reach 3 already and cost of paths 1 -> 2 -> 3 -> 5(new) < 1 -> 2 -> 5(existing path known), so update the cost and path to reach 5
Cost of reaching 6 via 4 is 4+1+2+5 and this is more than 1 -> 2 -> 3 -> 6, so do not update the cost and path to reach 6

iter:3

To visit:[[7], [5, 7]] in order (children of unvisited nodes only to avoid repetition)
Cost of reaching 7 via 5 is 4+1+5+6 and this is first time we are visiting the node, so store the cost and path to reach 7
Cost of reaching 5 via 6 is 4+1+4+1 and this is same as 1 -> 2 -> 3 -> 5, so do not update the cost and path to reach 5
Cost of reaching 7 via 6 is 4+1+4+8 and this is more than 1 -> 2 -> 3 -> 5 -> 7, so do not update the cost and path to reach 7

Task description

Find the only route from planet Erde to b3-r7-r4nd7 i.e, node 18 to node 246 among 1000 planets and 1500 routes possible in a bidirectional graph/map which allows moving from one planet to another with every route being associated with a cost value.

Working of code

-> Works based on Dijkstra’s algorithm of single source and single destination

-> Planets are visited based on least cost basis. The sub planets are recursively visited after one complete sweep again in least cost basis.

-> Relaxation, current cost, current node, actual path of every planet is kept track in a matrix

-> Execution stops when we reach our destination i.e, planet 246 or the planet named b3-r7-r4nd7

Result

Path to the destination planet is: [ 18 810 595 132 519 71 432 246]
Cost to reach the destination planet is: 2.995687895999458

{"source":18,"target":810,"cost":0.04060214221510905}
{"source":595,"target":810,"cost":0.1628038931266662}
{"source":132,"target":595,"cost":0.6331384762650787}
{"source":132,"target":519,"cost":0.6333618615566976}
{"source":71,"target":519,"cost":0.7625760415706333}
{"source":71,"target":432,"cost":0.6742157893614655}
{"source":246,"target":432,"cost":0.08898969190380779}

JSON data

Summary

In total there are 1000 Nodes and 1500 bidirectional paths

Every node has the following properties.

Original provided json

"nodes": [{"label":"node_0"}]
"edges": [{"source":343,"target":801,"cost":0.8117216039041273}]

Modified json to visualise with sigma

"nodes": [{"color": "#000000",
           "label": "0",
           "y": -2.3181617858307746,
           "x": 1.2953878183376322,
           "id": "0",
           "size": 0.02775471971630339}
"edges": [{"source":343,"target":801,"cost":0.8117216039041273}]

Data types conversion table between JSON <-> Python

 |  +---------------+-------------------+
 |  | JSON          | Python            |
 |  +===============+===================+
 |  | object        | dict              |
 |  +---------------+-------------------+
 |  | array         | list              |
 |  +---------------+-------------------+
 |  | string        | unicode           |
 |  +---------------+-------------------+
 |  | number (int)  | int, long         |
 |  +---------------+-------------------+
 |  | number (real) | float             |
 |  +---------------+-------------------+
 |  | true          | True              |
 |  +---------------+-------------------+
 |  | false         | False             |
 |  +---------------+-------------------+

 |  +-------------------+---------------+
 |  | Python            | JSON          |
 |  +===================+===============+
 |  | dict              | object        |
 |  +-------------------+---------------+
 |  | list, tuple       | array         |
 |  +-------------------+---------------+
 |  | str, unicode      | string        |
 |  +-------------------+---------------+
 |  | int, long, float  | number        |
 |  +-------------------+---------------+
 |  | True              | true          |
 |  +-------------------+---------------+
 |  | False             | false         |
 |  +-------------------+---------------+
 |  | None              | null          |
 |  +-------------------+---------------+