Sparse images/matrices are those in which the contained useful information is less compared to total space being occupied.
To begin with, we will look at an example image/matrix, the output we need and the main take aways from this post.
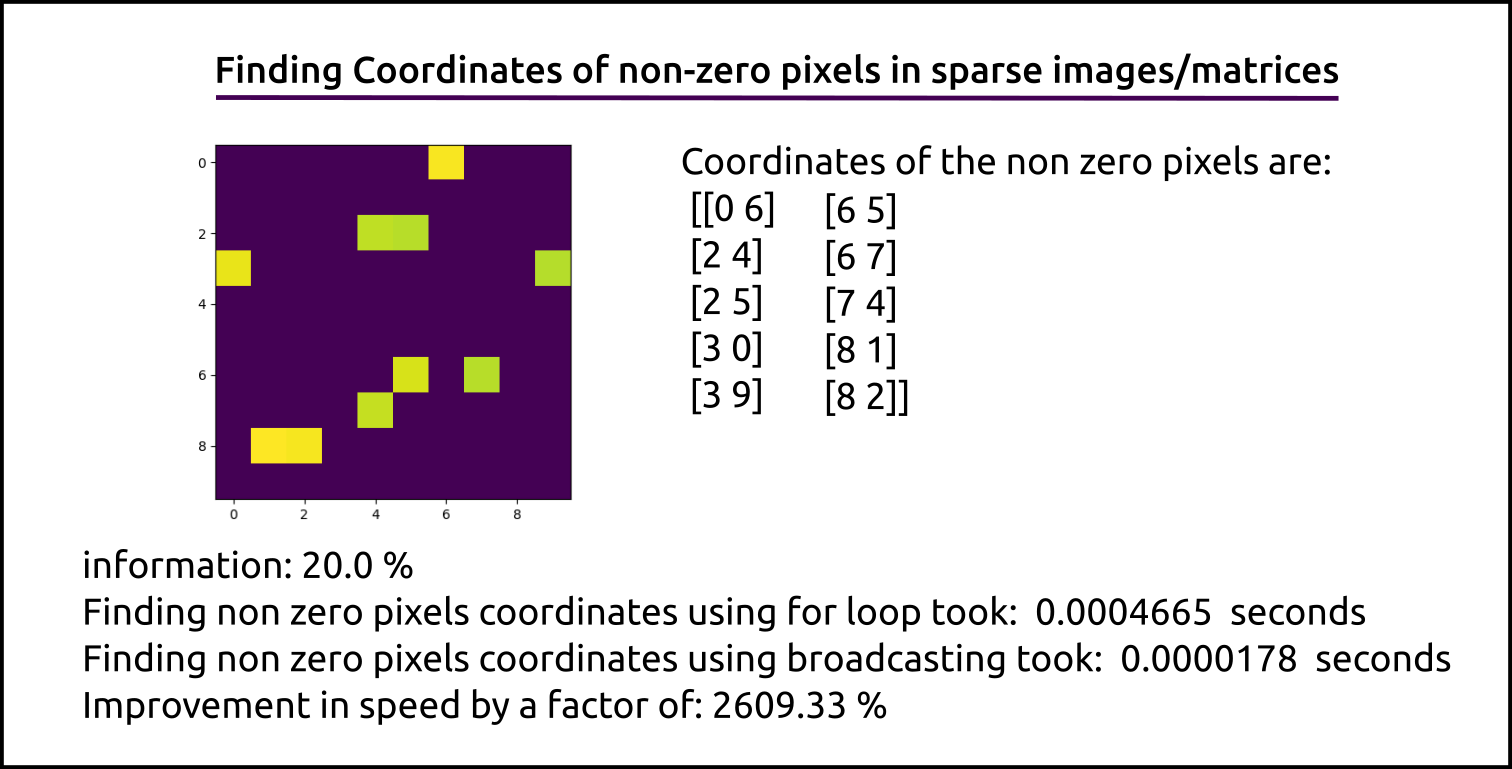
Task: To determine the (row, column) values of all the non zero pixels in a matrix or an image. Typical example would be text in a image. If you are familiar with the well known MNIST Handwritten digits dataset, that could be another good example of a sparse image
Note: The threshold need not be zero and can be any arbitrary value of interest
Example images that we will be working with

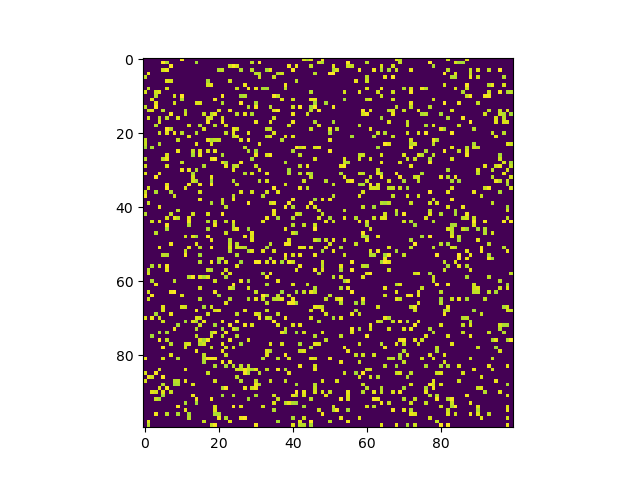
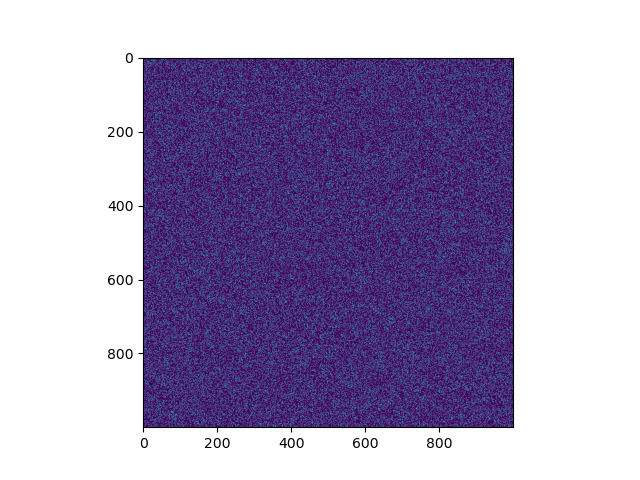
We will be going through two approaches in this short tutorial and also see how the methods compare in execution time
Method 1: The traditional and the first approach that comes to mind through for loops
Method 2: We can leverage the broadcasting properties of numpy and find a work around to reach the same result
Libraries used
- matplotlib
- time
- numpy
Pre Prep
First we need to create a sparse image to work with
import time
import numpy as np
import matplotlib.pyplot as plt
# Image height and width dimensions
rows = 100
columns = 100
img = np.random.rand(rows, columns) # Drawing number from uniform distribution [0,1] to avoid negative values
img = img * 255
img[img < 220] = 0 # this is optional and can be skipped to handle any threshold other than 'non zero value' & 'zero'
img = img.astype(np.uint8)
print(f"sparsity: {len(img[img != 0]) * 100 / np.cumproduct(img.shape)[-1]} %")
Method 1
x_coords = np.array([]) # To store column values
y_coords = np.array([]) # To store row values
start = time.time()
for r in range(rows):
for c in range(columns):
if img[r][c] != 0:
x_coords = np.concatenate((x_coords, np.array([c])))
y_coords = np.concatenate((y_coords, np.array([r])))
x_coords = x_coords.reshape(-1, 1)
y_coords = y_coords.reshape(-1, 1)
coords = np.hstack((y_coords, x_coords))
print("Finding non zero pixels coordinates with for loops took: ", time.time() - start, " seconds")
Method 2
First we create a template to go with our image dimension and make a boolean mask which we use to find the non zero pixel coordinates
coordinates_grid = np.ones((2, rows, columns), dtype=np.int16)
coordinates_grid[0] = coordinates_grid[0] * np.array([range(rows)]).T
coordinates_grid[1] = coordinates_grid[1] * np.array([range(rows)])
start = time.time()
mask = img != 0
non_zero_coords = np.hstack((coordinates_grid[0][mask].reshape(-1, 1),
coordinates_grid[1][mask].reshape(-1, 1)))
print("Finding non zero pixels coordinates using broadcasting took: ", time.time() - start, " seconds")
# print("Coordinates of the non zero pixels are:\n", non_zero_coords)
plt.imshow(img)
plt.show()
Results
sai@sai:~/****/scripts$ python coordinates.py 10 10
information: 13.0 %
Finding non zero pixels coordinates with for loops took: 0.0003330707550048828 seconds
Finding non zero pixels coordinates using broadcasting took: 3.4809112548828125e-05 seconds
sai@sai:~/****/scripts$ python coordinates.py 100 100
information: 13.43 %
Finding non zero pixels coordinates with for loops took: 0.024660587310791016 seconds
Finding non zero pixels coordinates using broadcasting took: 0.00010442733764648438 seconds
sai@sai:~/****/scripts$ python coordinates.py 1000 1000
information: 13.7047 %
Finding non zero pixels coordinates with for loops took: 8.874347448348999 seconds
Finding non zero pixels coordinates using broadcasting took: 0.007306575775146484 seconds
Conclusions
It is clear that the execution times differ significantly and the benefits become more dominant as the input data grows.